2025-02-13

数学オリンピック本選2025 第3問

数学オリンピック

条件を満たす整数の組の集合 $S$ をとる.

$1\leq a\leq100$ に対し数列 $a,a,a,…$ は $(a,a,a)$ のみを含むので $(a,a,a)\in S$ である.

$1\leq a\lt b\leq100$ に対し数列 $a,a,b,a,a,b,…$ は $(a,a,b),(a,b,a),(b,a,a)$ のみを含むのでこれらのうちの少なくとも $1$ つは $S$ に含まれる.

$1\leq a\lt b\leq100$ に対し数列 $a,b,b,a,b,b,…$ は $(a,b,b),(b,a,b),(b,b,a)$ のみを含むのでこれらのうちの少なくとも $1$ つは $S$ に含まれる.

$1\leq a\lt b\lt c\leq100$ に対し数列 $a,b,c,a,b,c,…$ は $(a,b,c),(b,c,a),(c,a,b)$ のみを含むのでこれらのうちの少なくとも $1$ つは $S$ に含まれる.

$1\leq a\lt b\lt c\leq100$ に対し数列 $a,c,b,a,c,b,…$ は $(a,c,b),(b,a,c),(c,b,a)$ のみを含むのでこれらのうちの少なくとも $1$ つは $S$ に含まれる.

以上の組に重複はないので $|S|\geq 100+{}_{100}C_2\times 2 + {}_{100}C_3\times 2=333400$ である.

逆に $S=\{(a,b,c)|1\leq a,b,c\leq100,a=b=cまたは(a\leq bかつb\gt c)\}$ とすると $S$ が条件を満たすことを示す.

$1$ 以上 $100$ 以下の整数からなる数列で $S$ に対して条件を満たさないようなものがあると仮定し, $a_1,a_2,\dots$ とする. このとき値は全て $1$ 以上なので単調減少ではなく, つまり $a_m\leq a_{m+1}$ となるような $m$ がある. このとき仮定から, $a_{m+1}\leq a_{m+2}$ であり, よって同様に考えると帰納的に任意の $k\geq m$ で $a_k\leq a_{k+1}$ となる. さらに仮定から任意の $k\geq m$ で $a_k=a_{k+1}=a_{k+2}$ ではないので $a_k\lt a_{k+2}$ となる. つまり $m$ 項目以降の偶数項目だけを見ると単調増加だが, 値は全て $100$ 以下なので矛盾. よってそのような数列は存在しない.

したがって $S$ は条件を満たし, さらに $|S|=333400$ であることも容易に分かるので最小値は $333400$ である.

感想

構成に気づけば簡単だが見つけるのが難しい.

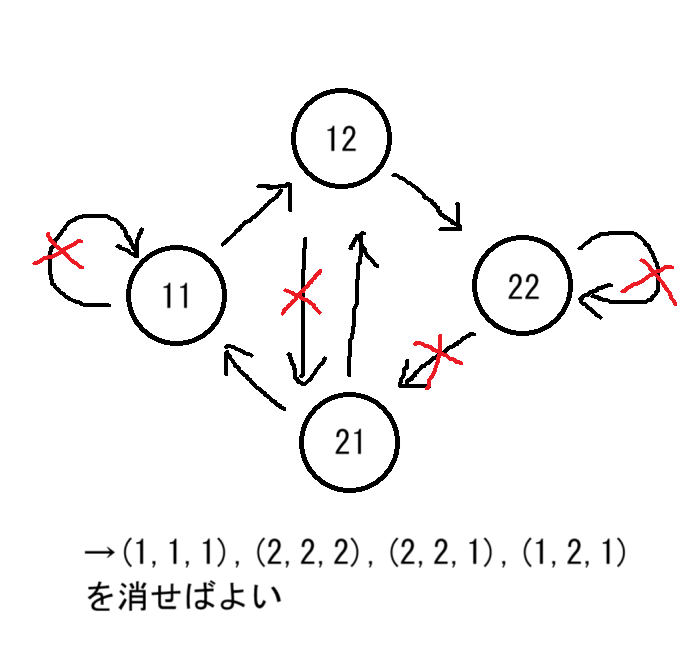
$1$ 以上 $2$ 以下の場合と $1$ 以上 $3$ 以下の場合についてまず考え, 末項 $2$ 項の組み合わせを頂点とした遷移図(有向グラフ)を書いてループが出来ないようなものを頑張って作ることで構成し, その結果を眺めていたら思いついた.

2025-02-12

数学オリンピック本選2025 第1問

数学オリンピック

議論の簡便化のため $a_{2n+1}=a_1$ とする.

与式の値が $2$ 未満だと仮定する.

仮定から $|a_i-a_{i+1}|\geq1$ となるような $1\leq i \leq 2n$ は $1$ 個以下である. よって必要ならば添え字を適切にシフトさせることで与式の値を変えずに $|a_i-a_{i+1}|\lt 1 \: (1\leq i \leq 2n-1)$ とできる.

ここで必要ならば $a_i$ 全体に $-1$ を掛けることで与式の値を変えずに $a_1+1\leq a_{n+1}$ とできる. このとき, $|a_1-a_{2}|\lt 1,\: |a_{n+1}-a_{n+2}|\lt 1$ より, $a_2-1\lt a_{n+2}$ であるので, 条件から $a_2+1\leq a_{n+2}$ である. 同様にして帰納的に $a_i+1\leq a_{n+i}\: (1\leq i \leq n)$ が得られる.

以上より $a_n=a_0+b,\: a_{n+1}=a_0+1+c, \: a_{2n}=a_n+1+d=a_0+b+1+d \: (c,d\geq0)$ とおけて, さらに仮定から $|a_{n}-a_{n+1}|\lt 1,\: |a_{2n}-a_0|\lt \sqrt{2}$ なので, 特に $|b|\lt 1$ である.

したがって $(a_{n}-a_{n+1})^2+(a_{2n}-a_{0})^2=(c+1-b)^2+(d+1+b)^2\geq (1-b)^2+(1+b)^2=2+2b^2$ が得られるが, これは仮定に矛盾.

ゆえに与式の値は $2$ 以上であり, さらに $a_0,\dots, a_n=0,\: a_{n+1},\dots, a_{2n}=1$ のとき与式の値は $2$ をとるので, 最小値は $2$ である.

感想

一番の割には難しくない？一瞬2/nが最小値にも見える.

2024-08-12

「クソデカスロン―現代十種― in パリ」解説

A:なぞなぞ

死に場所のオリンピック会場どーこだ？

死に場所を死地と言い換え、死をタヒと読むことでタヒチとなります。パリオリンピックのサーフィン競技が行われた会場はタヒチなのでこれが答えです。

答え:たひち

※セーヌ川は不正解です。

B:再翻訳なぞなぞ

二番目にハンドルを握る夏の風物詩は何ですか？

元の問題文:後手が運転をする夏の風物詩ってなーんだ？
翻訳後:Quelle est la tradition estivale de la deuxième personne au volant ?

後手が運転をするので、先手つまり先攻はナビゲーションをします。

答え:せんこうはなび

C:AI作成なぞなぞ

お金持ちのネズミはどこの場所にいる？

作ったAI本人に聞くと2回に1回ぐらい正解してくれます。

答え:ちゅーりっち

AIなぞなぞコンテストを開こうと思ってChatGPTで数百問生成したなかで一番まともだった問題です。

D:合体漢字

"㍈一丶八六円旧툐

「ダブルクォーテーション」「ミクロン」「イチ」「チュ」「ハチ」「ロク」「エン」「キュウ」「ティョ」

この文字たちを合体させて2文字の言葉を完成させよ！

まずは1文字目、合体！！

ホウ！

続いて2文字目、合体！！

リョウ！

さらに合体！！！

ホウリョウ！！！

答え:豊漁

E:手描き謎解き

海と海岸と人が描かれたイラストです。人が海の上で本を読めるぐらい浮力が大きいようです。つまり死海のイラストです。画像は死海の海岸線を指しているようです。死海は湖なのに海岸線と言ってよいのでしょうか？。言うとします。「しかい」の「かい」が「んせん」なので答えは「しんせん」です。

※「しかい」の「かい」が「ん」で「しん」は不正解とします。

答え:しんせん

F:数列推理

7,11,?

注意に「表記の指定がない場合はひらがなで解答してください。」とあるので当然ひらがなで解答する問題です。

セブンイレブンが1976~2011年にCMで使用していた「セブン、イレブン、いい気分」というキャッチコピーが当てはまるので答えは「いい気分」です。

答え:いいきぶん

10代とかだと知らない可能性があるかもしれません。クソデカスロンなのでそういうこともある。

G:AI画像なぞなぞ

元の問題文:解法が分からない教科なーんだ？

解き方が分からない、つまり「どう解く？」です。

答え:どうとく

H:聖徳太子なぞなぞ

https://drive.google.com/file/d/1sQGaGqNm6-p3o5xeiYDSr49bwlKmG8xv

それぞれ「明海(冥界)大学」「大正(大将)大学」「明星(名声)大学」「目白(メジロ)大学」です。

これらはご存知、大学群「明明大工目」に含まれる大学です。よって残りの東京工芸大学が答えです。

答え:とうきょうこうげいだいがく、とうきょうこうげい

I:AI解答なぞなぞ

ChatGPT「フーリガン」

Gemini「冷蔵庫の詩人」

Copilot「ソロクック」

元の問題文:社会不適合者の料理人ってなーんだ？

社会不適合者は社不と略されます。これはシェフに似ています。

答え:しゃふ

Geminiはこのあと独創的な答えを10個ぐらい出してきて怖かったです。

AIを使った問題は3問目ですが十種競技も投擲種目だけで3種目あるので大体同じです。

J:ソート行列推理

それぞれの盤面はソートされているようです。よって解答盤面もソートされていると考えられます。ペナルティはないので10通り総当たりすると正解できます。

答え:000001111

元の問題です。行BC300点ぐらいの通常の行列推理なのでよかったらどうぞ。

あとがき

優勝は4問正解でnvx99sさんでした。

nvx99sさんにはキング・オブ・カスリートの称号が与えられます。おめでとうございます！

次回4年後に行われる「クソデカスロン―現代十種― in ロサンゼルス」でお会いしましょう。それでは。

2024-02-11

数学オリンピック本選2024 第2問

数学オリンピック

任意の $m$ をとり, $f(m)\lt p$ かつ $\gcd(f(m),p)=1$ であるような素数 $p$ をとって, $n=p-f(m)$ とおく.

このとき $m|\text{lcm}(m,f(m+f(n)))=\text{lcm}(f(m),f(m)+n)=\text{lcm}(f(m),p)|f(m)p$ .

よって任意の $m$ に対して $m|f(m)$ が得られる.

次に $m=1$ , $n=f(1)$ とすると,

$f(1+f(1))=\text{lcm}(m,f(m+f(n)))=\text{lcm}(f(m),f(m)+n)=\text{lcm}(f(1),2f(1))=2f(1)$ .

前の議論から,ある自然数 $a$ により $f(1+f(1))=a(1+f(1))$ とおけるが, $a\geq 2$ と仮定すると, $2+2f(1)\leq a(1+f(1))=2f(1)$ より矛盾.

したがって $a=1$ であり, $1+f(1)=f(1+f(1))=2f(1)$ から $f(1)=1$ .

次に $m=1$ とすると,

$f(1+f(n))=\text{lcm}(m,f(m+f(n)))=\text{lcm}(f(m),f(m)+n)=\text{lcm}(1,1+n)=1+n$ .

前の議論から, $f(n)=an$ , $f(1+f(n))=b(1+f(n))$ とおくと $b+abn=1+n$ が得られ,結局 $a=b=1$ が必要.特に $f(n)=n$ が得られる.

逆に $f$ を $f(n)=n$ とすれば,両辺は $\text{lcm}(m,m+n)$ と等しいことが分かるので条件を満たす.

したがって求める関数は $f(n)=n$ のみである.

感想

あんまり見ないタイプの関数方程式だなあと思った.

2024-02-11

数学オリンピック本選2024 第1問

数学オリンピック

以下 $a_0$ は $a_{n}$ を, $a_{n+1}$ は $a_1$ を指すものとする.

$\{a_i\}$ の中で絶対値が最大なものの1つを $a_k$ と置く.

・ $a_k$ が正の場合.

$a_{k-1}\lt a_{k}$ だとすると

$|a_{k-1}-2a_{k}|=2a_{k}-a_{k-1}=a_k+(a_{k}-a_{k-1})\gt a_k=|a_k|$ であり矛盾.

よって $a_{k-1}= a_{k}$ .

これを繰り返すことで $\{a_i\}$ は全て等しいことが分かる.

・ $a_k$ が負の場合.

$a_{k-1}\gt a_{k}$ だとすると

$|a_{k-1}-2a_{k}|=a_{k-1}-2a_{k}=(a_{k-1}-a_k)-a_k\gt -a_k=|a_k|$ であり矛盾.

よって $a_{k-1}= a_{k}$ .

これを繰り返すことで $\{a_i\}$ は全て等しいことが分かる.

・ $a_k$ が0の場合.

$\{a_i\}$ は全て0なので全て等しい.

したがっていずれの場合も $\{a_i\}$ は全て等しいことが分かった.

これを $a$ とおくと条件から $a-2a=a$ が必要であり,つまり $a=0$ である.

ゆえに条件を満たすのは $\{a_i\}$ が全て $0$ の場合のみである.

感想

和が0になることぐらいはすぐに分かるしどうせ全部0の場合しかなさそうと思えるがその後の発想が少し難しい.思いつけば記述は簡単そう.

2023-08-10

競プロerが応用情報を受けた所感

ちょっと書いて面倒で放置してたら公開がこんな時期に…

伝えたいこと

・競プロerで受ける人はnok0さんのブログを参考にしましょう。

tsuchi.hateblo.jp

・午前は4割ぐらいは応用情報の過去問から出ます。それに加えて基本情報の過去問とかからも多少出るので過去問道場で過去問を回しまくるだけでいいです。

・午後は競プロerなら緑レート以上あれば大して対策しなくても通りそうな気がしました。

以下蛇足

スペック

・数学系の修士1年

・AtCoder黄

・学部の講義は文字通り片っ端から受けたので情報系の講義もそれなりにとっていた

受験まで

過去問を解いたら6割とれたので受けようかな～という気分になりました。

暇つぶしに応用情報技術者の過去問50問といたらちょうど6割とれたから春にでも受けようかな
ちょっと勉強すれば受かりそう pic.twitter.com/DOY5PpjXiK
— ねしゃ～ (@yuui_nesya) 2022年9月29日

基礎理論が全部とれてるのは学部の講義で習った内容とある程度被っているというのもあったと思います。

試験1か月前ぐらいまで何もやっていなくて流石に何かやった方がいいかな～と思っていたら、TOEICで500点だか600点だかとらないと卒業できなくてヤバい！って言っている友人が一緒に集まって勉強しようと言ってきたので勉強することにしました。

参考書についてですが、受験料で7500円も払ってるのにさらに金を払うのも馬鹿らしかったのでなんかいい方法ないかな～と思ったんですが、Maruzen eBook Libraryの大学で契約している本の中に応用情報の参考書があったのでそれを無料で読みました。「徹底攻略応用情報技術者教科書」ってやつです。

勉強方法としては、参考書を読み進めつつそれに対応する過去問を分野指定で解くのを繰り返しました。テクノロジ系は参考書を読んでいて多少は意味があったような気がしましたがマネジメント系とストラテジ系はあんまり意味がなかった気がします。参考書もそこの部分は適当に読み飛ばしました。

午後は前日まで対策しておらず、前日にnok0さんのブログとか同じ回を受ける友人の意見を参考にし、プログラミングと組込みシステム開発とシステム監査をとることにしてもう一つは会場で簡単そうなものを選ぶことにしました。

試験の感触

午前

思ったより過去問から丸々でているものが多いなと思いました。(実際かなりの割合が過去問の流用らしい。)

過去問を解いていた感じだと8割は確実にとれると思っていたのですが、今回のは難易度が高く解いていて7割ぐらいかな～となりました。

ドップラー効果の利用法みたいな問題もあってこんなの出るんだと思いました。

午後

情報セキュリティ…英語の略称を答える問題が2問ありしらね～～となり両方とも完全に勘になったし両方間違えた。

プログラミング…10分ぐらいで片づくと思ったが意外に手間取り30分ぐらいかかったがさすがに全完。

組込みシステム開発…問題文に書いてある仕様をちゃんと読めますかというだけで簡単だった。

システム監査…ただの国語でだいぶ簡単に思えたが、設問が嘘かと思うぐらい少なく1問間違えただけでだいぶ点が飛びそうで怖かった。

このあとどれを選択するか迷ったが計算問題が見え他の問題も大体解けそうだったシステムアーキテクチャを選択

システムアーキテクチャ…データ形式を答える問題で唯一知っているCSVと答えたら間違えた。ほとんど読めば解ける問題だと思って選んだが最終問題が普通に知識がなく見当違いなことを書いて終了。

結果

午前:71.25点

午後:89.00点

でした。

応用情報技術者試験合格しました！ pic.twitter.com/on8YEewMj5
— ねしゃ～ (@yuui_nesya) 2023年6月29日

午後は

情報セキュリティ 16/20
プログラミング 20/20
システムアーキテクチャ 14/20
組み込みシステム開発 19/20
システム監査 20/20

ぐらいの感触です。

感想

ノー勉でいけるやろｗとか思ってたんですがこの難易度だと午前は勉強してなかったら落ちていた気がするので勉強しておいてよかったです。

午後は競プロをやってるならある程度問題文の読解もできるはずで、プログラミング・組み込みシステム開発・システム監査は高得点が取れるんじゃないかと思いました。もう1つは適当に選んでください。

解答例を出している会社が複数あり試験後に眺めていたんですが、システム監査の解答例が記号問題すらめちゃくちゃに割れていて面白かった。ただの国語の問題だと思ったけど思ったより難しいのかもしれない。

一緒に勉強していた友人はTOEICの点が全然足りなかったけど大学の救済用の試験を受けて無事単位が取れたらしいです。

2023-02-18

ねしゃ～

この記事の項目名には以下のような表記揺れがあります。

ねしゃ～

ねしゃー

ねしゃ

ネシャア

ネシャー

nesya

Nesya

nesya-

Nesya-

nesya~

Nesya~

nesyã

Nesyã

Nesyarote

Nesyarlathotep

涅紗亞

📝この項目「ねしゃ～」は、内容をより充実させるため、加筆が求められています。